Improve performances
# Improve the Performances
There are many ways to improve the performances of a simulation. This page provides a few tips to help achieving this goal.
Compilation Options
On Windows, the two following CMake variables may speed up the simulations:
SOFA_ENABLE_FAST_MATH: Enable floating-point model to fast (theoretically faster but can bring unexpected results/bugs)SOFA_ENABLE_SIMD: Enable the use of SIMD instructions by the compiler (AVX/AVX2 for msvc).SOFA_ENABLE_LINK_TIME_OPTIMIZATION: Enable LTCG IN release mode [Warning, use a lot of disk space!]
RunSofa
When running runSofa with the GUI, an option allows to update the visual representation of the scene graph if any change is detected (activated by default). It can affect badly the performances in high speed simulations. Disabling the option can help improving the performances: to do so, click on the lock icon as illustrated below.
Profile the Simulation
The first step toward better performances is to identify the bottleneck of the simulation. SOFA provides some tools to profile the simulation. See this page to learn how to use those tools. The principle is to measure the time taken by all major steps of the simulation. The timers are organized as a tree: a monitored step can call monitored substeps, making it a parent of the substeps.
Let us take the example of the caduceus demo, located in examples/Demos/caduceus.scn. The following image results from the profiling of one time step, measured in the GUI of runSofa.
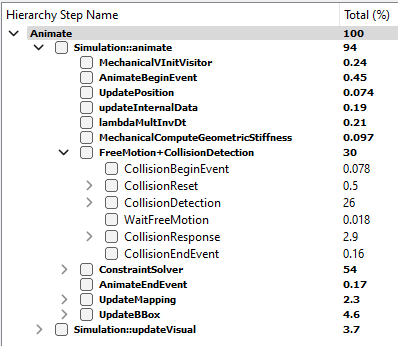
Two major steps can be identified:
1) FreeMotion+CollisionDetection 2) ConstraintSolver
Together, both steps account for 84% of the total computational time spent in the simulation step. In most simulation, those two steps will be the most time-consuming.
As the name suggests, the step FreeMotion+CollisionDetection gathers two substeps:
1) The collision detection 2) The free motion
These steps and their associated timers are specific to the FreeMotionAnimationLoop. Its particularity is that those two steps can be computed in parallel. It is the case in the example: collision detection takes 26% of the time. During that time, the free motion is computed in parallel. That is why the timer WaitFreeMotion is almost null. This parallelization is a possible solution to optimize the performances of this simulation. This parallelization is available because the computation of the free motion is also a time-consuming step of a simulation.
To summarize, the 3 major steps of a simulation, candidates for being a bottleneck, are:
1) Collision detection 2) Free motion 3) Constraint solving
In each of them, some substeps can be responsible of the bottleneck. The profiler helps identifying the one(s) . In the above example, the most time-consuming step is constraint solving, taking 54% of the time.
Collision Detection
If collision detection has been identified as a bottleneck, here are a few tips to improve the performances:
Asynchronous Free Motion
This tip requires to use a FreeMotionAnimationLoop.
The steps of collision detection and free motion are independent: they can be computed in parallel. The component FreeMotionAnimationLoop has boolean Data parallelCollisionDetectionAndFreeMotion to specify if both steps are computed in parallel or not. This optimization is the most effective when both steps takes about the same time. The total time of both steps computed in parallel will be the time taken by the most time-consuming one (plus the overhead due to parallelization).
Parallel Algorithms
There are high chances that a simulation uses BruteForceBroadPhase and BVHNarrowPhase. Multi-threaded versions of those two components are available in the MultiThreading plugin. Depending on the cases, the parallelization can help speeding up the collision detection phase. See details in the MultiThreading plugin dedicated page.
Free Motion
This step is computed in the FreeMotionAnimationLoop. However, there are also common steps with the DefaultAnimationLoop, such as the computation of the force, the matrix assembly and the resolution of the linear system. Therefore, most of the tips of this section are also available for DefaultAnimationLoop.
The Choice of the Linear Solver
See this page for a description of the different types of linear solvers.
Iterative Solvers
The error reduces at each iteration of an iterative solver. Some of the parameters (e.g. iterations, tolerance and threshold in CGLinearSolver) controls when the solver stops its iterations. Less iterations means less computation, therefore faster simulations. Stopping too early can come at the price of too large error, and can even bring instabilities. With iterative solvers, finding an appropriate trade-off between accuracy and efficiency is key.
Matrix Assembly
Assembling by blocks: When the linear solver assembles the system matrix in a compressed sparse row data structure, it is possible to use a matrix where the entries are blocs of 3x3.
This is much faster to assemble.
It is the most efficient when the simulation only involves 3 degrees of freedom per node (known as "Vec3d" in the SOFA template).
The template parameter to use is CompressedRowSparseMatrixMat3x3d.
Note that all solvers do not support this template parameter.
Parallel assembly of independent matrices: Mapped components contributes to a matrix data structure different from the main matrix.
Once they are assembled, the mapped matrices are projected into the main DoFs space via mappings jacobian matrices.
Since the main matrix and the mapped matrices are independent, they can be assembled in parallel.
To activate this option, enable the Data parallelAssemblyIndependentMatrices in MatrixLinearSystem.
Matrix Assembly vs. Matrix Free
CGLinearSolver supports both strategies:
GraphScatteredis the template parameter for a matrix-free solverCompressedRowSparseMatrixdandCompressedRowSparseMatrixMat3x3dare template parameters for an assembled matrix
It is not always obvious which one is faster given the same number of iterations.
However, it is easy to try both strategies: just change <CGLinearSolver template="GraphScattered"/> to <CGLinearSolver template="CompressedRowSparseMatrixMat3x3d"/>, and vice-versa, and compare the performances.
Asynchronous Linear Solver
SparseLDLSolver has an asynchronous equivalent (AsyncSparseLDLSolver), which the goal is to reduce the duration of the linear system solving.
Computing asynchronously the LDL factorization of the matrix, this solver will however change the behavior of your simulation.
Read more about it on the AsyncSparseLDLSolver page.
In your scene, just replace <SparseLDLSolver/> by <AsyncSparseLDLSolver/>.
Constant Sparsity Pattern
Usually, the linear system resulting from a simulation is sparse, meaning that a significant portion of the elements of the system are zero. Thus, an efficient representation where only non-zero elements can be considered to speed up computations. Moreover, in specific scenarios, this sparsity maintains a constant pattern. In other words, the arrangement of zero and non-zero elements within the system does not change as the simulation progresses from one time step to the next. The simulation computation can take advantage of this time-consistent sparsity, as it allows for the use of precomputed data related to the structure of the system, thereby optimizing the overall efficiency of the simulation.
Situations in which the sparsity pattern is not constant include the following:
- Topological Changes: changes in the structural or system topology can lead to alterations in the sparsity pattern of a matrix. This occurs when new elements or connections are introduced or existing ones are removed.
- Changes in the application of forces to degrees of freedom (DoFs) can directly impact the sparsity pattern of a matrix. When a force is newly introduced to a DoF that was previously uninvolved, it may lead to the addition of new non-zero entries in the matrix, thus altering the sparsity pattern. Conversely, if a force is removed from a DoF that was previously under its influence, it may result in the elimination of non-zero entries associated with that DoF, consequently causing changes in the sparsity pattern of the matrix.
- Boundary Condition Changes: Altering boundary conditions, such as fixing or releasing certain degrees of freedom, can modify the sparsity pattern.
In these scenarios, where the sparsity pattern is not constant, traditional compression techniques may be required to handle the dynamic nature of the system.
Block Tridiagonal Matrix:
Dealing with linear structures like wires or beams leads to a specific type of mathematical representation known as a block tridiagonal matrix (BTD). This matrix structure exhibits distinct characteristics, with a pattern of non-zero elements only on the main diagonal, the superdiagonal (one diagonal above the main diagonal), and the subdiagonal (one diagonal below the main diagonal).
To address this particular matrix format effectively, a specialized linear solver has been developed: BTDLinearSolver, and its associated matrix format BTDMatrix.
This dedicated solver significantly outperforms the use of a generic linear solver that lacks the specialized algorithms and optimizations enabled by block tridiagonal matrices.
Constant Insertion Order In generic scenarios where the sparsity pattern of a matrix is not predetermined, it is common practice to accumulate contributions within a matrix data structure. This matrix data structure is often designed with a compressed format, which is intended to reduce memory usage and computational overhead. However, this compression process can be time-consuming, particularly for large-scale problems. There are specific situations where it is possible to optimize the matrix assembly process by avoiding the compression step. This optimization is applicable when the following conditions hold:
- Constant Sparsity Pattern: the sparsity pattern of the matrix remains fixed throughout the problem-solving process. In other words, the locations of non-zero elements in the matrix do not change.
- Constant Insertion Order: the order in which contributions are inserted into the matrix remains consistent over time. Contributions are added to the matrix in a predetermined order.
- Mapping between Insertion Location and Compressed Format: a mapping exists that relates the location of insertion (where contributions are added) to the location of the contribution in the compressed format of the matrix. This mapping ensures that contributions are placed directly in their appropriate positions in the compressed matrix without the need for a compression step. This mapping is computed automatically in the first matrix assembly.
In such scenarios, the 'ConstantSparsityPatternSystem' component is a valuable tool. By using this component, it becomes possible to expedite the matrix assembly step. This can lead to significant performance gains.
Parallel ODE Solving
This optimization requires to use a FreeMotionAnimationLoop. When multiple objects evolve in a simulation, SOFA supports the following configurations:
- There is a single ODE solver for all the objects.
- There are multiple ODE solvers, and each one can simulate one or multiple objects.
In the latter case, there are as many free motion computations as the number of ODE solvers in the scene. In this first step of the FreeMotionAnimationLoop, the free motion assumes that objects can have a "free" motion, thus ignoring possible interaction between objects. Therefore, the computation of the free motion of an object is independent from the others, and each ODE solve step can be trivially parallelized. The component FreeMotionAnimationLoop has boolean Data parallelODESolving to specify if both ODE solve steps are to be computed in parallel or not.
Finite Element Method
Several algorithms are available to simulate the same FEM model, so the simulation designer can choose depending on the constraints on the accuracy and speed of the simulation.
For example, a component can have an alternative where the implementation uses approximations in order to speed up the computations.
This is the case for the component TriangularFEMForceFieldOptim which is an alternative to TriangularFEMForceField.
It has been measured that TriangularFEMForceFieldOptim is faster than TriangularFEMForceField.
Similarly, the component FastTetrahedralCorotationalForceField is a faster alternative to TetrahedronFEMForceField, but without any compromise on the accuracy.
Parallel Constraint Solving
The following options allow to leverage multi-threaded implementations of some algorithms:
parallelInverseProductinSparseLDLSolverallows to parallelize the computation of the product \(\mathbf{J}\cdot\mathbf{M}^{-1}\cdot\mathbf{J}^T\), which is used to compute the compliance matrix projected in the constraint space (seeLinearSolverConstraintCorrection).multithreadinginGenericConstraintSolverallows to build the compliances concurrently.
Rendering
-
A data
computeBoundingBoxis available in all AnimationLoops. This data defines whether the global bounding box of the scene is computed at each time step. Setting this data tofalsewill avoid the recomputation of the bounding box used for rendering, thus possibly saving computation time. -
Debug visualization can be very costly. For example, drawing thousands of tetrahedra is very time consuming. Draw only what you need.
Model Order Reduction
In SOFA, Model Order Reduction is a technique to reduce the computational complexity of a FEM simulation. It works with a premilinary step which precomputes deformation modes of an object. The modes are then used online, during a simulation, allowing to build and solve the same FEM problem in a reduced space, in order to dramatically increase the performances.
This technique is available in a plugin: https://github.com/SofaDefrost/ModelOrderReduction. Binaries are also available.
GPGPU
SOFA has a plugin allowing to compute some steps of the simulation on the GPU, based on CUDA. See this page. In most cases, the simulation is much faster when computed on the GPU, compared to the CPU version.